FORMULACIÓN DE HIPÓTESIS-NATURALEZA DEL ENSAYO DE HIPÓTESIS

En general en estadística las decisiones se toman sobre unas determinadas hipótesis.

Así por ejemplo, se tratará de tomar decisiones acerca de hipótesis tales como si un nuevo proceso de producción es más eficiente que  uno anterior, o si la proporción de personas favorables al divorcio ha aumentado, si un medicamento nuevo es  más efectivo, o cuál de dos sistemas de aprendizaje es mejor. Tales hipótesis se expresan siempre en función de un parámetro estadístico. Así la hipótesis de que una moneda no está cargada se expresaría como p=0,5   (p = proporción de caras en una serie de lanzamientos).

Pero no se puede estudiar directamente la hipótesis que entra en juego, sino que se trata el problema de forma indirecta. Lo equivalente a confirmar una hipótesis dada, es negar o rechazar su alternativa lógica. Para poder decidir sobre una hipótesis (que normalmente establecerá que existe una tendencia o relación en la población) , examinamos la contraria  a la que se denomina hipótesis nula ( que establecerá que no existe tal tendencia o relación ). En cada proceso de decisión, habrán de establecerse la hipótesis nula o hipótesis de partida  H₀ (que es la que se contrastará), y la hipótesis alternativa  H₁  (sobre la que se quiere decidir) complementaria de la anterior.

Para entender mejor el proceso, suele establecerse un paralelismo entre el contraste de hipótesis y el juicio a una persona. No se puede iniciar un proceso judicial tratando de demostrar la inocencia de una persona ( inocencia que estaría representada por la hipótesis nula). Tal inocencia se presupone. Lo que se hace en un juicio, es partir de la inocencia, y a la luz  de la o las pruebas , rechazar o no la presunción, aceptando o no la culpabilidad (hipótesis alternativa).

Tomaremos pues como cierta la hipótesis nula, y la mantendremos  hasta que no se demuestre lo contrario, es decir hasta que en un juicio se nos haga comprender la incompatibilidad de dicha hipótesis con las pruebas presentadas, de forma que tengamos evidencias suficientes para aceptar lo establecido en la hipótesis alternativa.

ESQUEMAS DE DECISIÓN

Dado que ‘la ausencia de evidencia no implica evidencia de ausencia’ , si las pruebas presentadas no son evidencia suficiente a favor de la hipótesis alternativa, en principio, el no rechazo de la hipótesis nula, no tendría porqué llevar aparejado la aceptación de lo establecido por dicha hipótesis.

En general, las hipótesis nulas se establecen con el ánimo de rechazarlas. Cuando tras obtener unos resultados muestrales que nos hacen formular una hipótesis de que “en la población total existe una determinada relación”  formularemos una hipótesis nula en el sentido de que “no existe tal relación en la población”, es decir que los resultados obtenidos en la muestra son debidos al azar y no a lo postulado por la hipótesis alternativa.  A partir de aquí, lo que interesa es saber si podemos aceptar o no (con una probabilidad  de error a llamada nivel de significación), la hipótesis alternativa.

Cuando el esquema es el descrito anteriormente, el esquema de trabajo que adoptamos es:

Existen sin embargo otros casos, en los que no es posible la indefinición sobre lo establecido en la hipótesis nula. En estos casos, el test debe dar lugar siempre a una decisión: aceptar H₁ o aceptar H₀. Se presentan las siguientes posibilidades:

Es decir, el esquema de decisión en este caso es :

REGLA DE DECISIÓN - PRUEBA DE CONTRASTE

Si ya están formuladas las hipótesis, ¿bajo que condiciones podrá ser rechazada la hipótesis nula?. O lo que es lo mismo, ¿cuando consideraremos que tenemos evidencias suficientes de la hipótesis alternativa?. Este es el momento de elegir la regla de decisión, es decir , establecer un criterio que permita rechazar o no la hipótesis nula.

Por lo general , una prueba o regla de decisión para contrastar una hipótesis consiste en un suceso o resultado experimental S, cuya posibilidad de ocurrencia  sea muy pequeña siendo cierta la hipótesis H₀, es decir:

                                                                            (Nivel de significación)

Si ocurre el suceso S, rechazaremos la hipótesis H₀,  y no lo haremos en caso contrario.

La justificación es simple: o bien la hipótesis es cierta y se ha producido un suceso de muy pequeña probabilidad, o bien la hipótesis es falsa. Es como si hiciésemos una reducción al absurdo, sólo que la contradicción con la hipótesis de partida no se establece de forma absoluta, sino en términos de probabilidad.

Si ocurre S, parece pues natural que apostemos por la segunda opción y rechacemos la hipótesis H₀, haciendonos cargo de que existe una probabilidad a (es la probabilidad de que haya ocurrido S aún siendo cierta H₀)  de equivocarnos.

Veremos ahora algunos ejemplos que nos permitirán aclarar lo antes expuesto:

EJEMPLO 1:

Supongamos que a n personas se les mide la presión sanguínea bajo el efecto de un medicamento y sin él. Sean las observaciones   e   . Diremos que el  i-ésimo ensayo es un éxito si x_i>y_i  y fracaso si x_i<y_i  ( para tener mayor simplicidad supondremos que no hay dos medidas que lleven al mismo resultado).  Si el medicamento no tiene efecto sobre la presión, nuestras observaciones corresponden a una B(n;½). Un suceso S que sirva como señal de que el medicamento afecta a la presión, podría ser que el número de éxitos fuera superior a n/2 . Es evidente que cuanto mayor sea el número de éxitos exigidos por S menor será el nivel de significación.

EJEMPLO  2:

Un método para rehabilitar alcohólico se sabe por experiencia que es efectivo en el 80% de los casos de cierta enfermedad. Un nuevo método que está siendo ensayado, ha rehabilitado a 89 de 100 pacientes elegidos al azar. Imaginemos que queremos tomar una decisión sobre la eficacia del nuevo método ( H₁: “El nuevo método es más efectivo que el anterior” ). Establecemos que H₀=”El nuevo método es igual o menos efectivo que el anterior”, y como suceso de prueba que S = ”Al realizar un muestreo, se obtiene al menos una efectividad del 89%”.

En términos de parámetros la efectividad del nuevo medicamento es la proporción p de pacientes que dicho medicamento cure, es decir:

Si suponemos cierto H₀ , el número X de éxitos (curaciones) en 100 intentos se distribuye según B(100;0’8) que es equivalente a N(80;4). Pero en tal caso , la probabilidad de que ocurra S sería:

[1]

Si establecemos un nivel de significación superior al 1,22%, deberemos rechazar H₀ (y en consecuencia aceptar que es más efectivo el nuevo método)  y no podremos hacerlo en otro caso.

EJEMPLO 3:

Dos amigos A y B, juegan a cara o cruz con una moneda. Lanzan una moneda en 100 ocasiones, y A que eligió cara ha ganado en 62 ocasiones. Tras este resultado, B afirma que la moneda está trucada, de forma que la probabilidad de obtener cara es 2/3, mientras A mantiene que la moneda es correcta y el resultado es debido al azar. Se te encarga dictaminar sobre cual de los dos tiene estadísticamente la razón.

Ahora debemos aceptar  obligatoriamente una de las dos hipótesis, es decir obrar de acuerdo al segundo esquema.

Establecemos las hipótesis:

Si X es el número de caras (éxitos) después de 100 intentos,  su distribución es una si es cierta H₀, y una  si es cierta H₁.

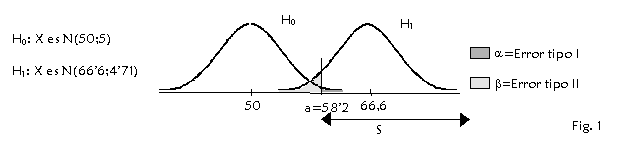
Supongamos cierta H₀ .De la Fig. 1, establecemos S como un intervalo de forma que

 de donde obtenemos que dicho intervalo será de la forma (a,100) , siendo:

p( X>a / H₀) = 0,05

En la tabla de la normal tipificada, p(Z>1,65)=0,05 y por tanto  .

Puesto que el resultado muestral es 62 podemos rechazar la hipótesis nula y aceptar que la moneda tiene una probabilidad de cara de 2/3.  Al tomar esta decisión nos equivocaremos en un 5% de los casos. (Error de tipo I o nivel de significación)

Si embargo si hubiéramos obtenido un resultado muestral de 57 caras, habríamos aceptado la hipótesis nula, y también tendríamos una probabilidad de error , el de tipo II. Para calcular dicha probabilidad, supongamos que H₁ es cierta. El error se producirá cuando un resultado muestral sea menor de 58.2 , pues entonces aceptaremos H₀ , y la probabilidad de que ello ocurra es:

b = p( X<a / H₁) =

Dado que muchos de los parámetros sobre los que se suele establecer un contraste de hipótesis tienen una distribución normal , la regla de decisión S queda determinada como en el ejemplo anterior, por una región, denominada región crítica o de rechazo que quedará a la derecha, izquierda o ambos lados de la distribución muestral del parámetro supuesta cierta la hipótesis H₀.

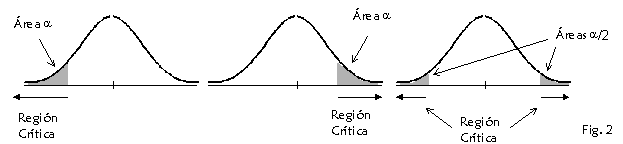
De esta forma, rechazaremos H₀ cuando se verifique S, es decir el estadístico (parámetro muestral) quede en esta región, y no lo haremos en caso contrario (Fig. 2).

LOS ERRORES

Podríamos decir en consecuencia que si queremos establecer  una prueba  para rechazar o no una hipótesis, deberemos de buscar un suceso de muy baja probabilidad (cuanto más baja, más específica[2] será la prueba) bajo la suposición  de veracidad de la hipótesis nula.

Para poder rechazar que  H₀ = ”una moneda no está cargada”, podríamos establecer  S = ”salen 65 o más caras al lanzarla 100 veces”, de forma que  a =0,13%   , es decir la prueba dará un resultado erróneo en  sólo 13 de cada 1000 casos. Si S = “salen 70 o mas caras”, es evidente que la prueba sería más específica

Sin embargo, tal y como se puede observar en la Fig. 1 , en general una disminución del riesgo a lleva aparejado un aumento del riesgo b, y cuanto mayor sea, en mayor número de casos se aceptará una falsa hipótesis nula , diciéndose en este caso que la potencia o sensibilidad del test disminuye[3]. En casos como el ejemplo 5 y en muchos otros en general, se podrán reducir ambos riesgos, si aumentamos el tamaño muestral, pues este aumento dará lugar a una menor variabilidad muestral.